The stochastic differential equation of the Wiener process has been generalized by Ito in the following way:

Hereby a generalized drift term b (X(t),t)dt has been added and the diffusion coefficient a itself has been generalized now depending on X. The solution X(t) is called Ito process.

For an Ito process X(t) it can be shown that also any image process y(t) = y(X(t), t) of the Ito process leads to an Ito process according to the below formula.

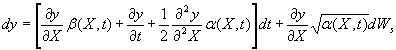
This is Ito’s formula which will be needed later. In contrast to conventional analysis the quadratic term cannot be neglected and hence does not disappear.